80 lines
2.8 KiB
Markdown
80 lines
2.8 KiB
Markdown
# 二叉树(Binary Tree)
|
||
|
||
> 🔔 参与讨论:https://www.isharkfly.com/t/binary-tree/15117
|
||
|
||
二叉树是一种非常重要的数据结构,很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树,有深度遍历和广度遍历,深度遍历有前序、中序以及后序三种遍历方法,广度遍历即我们平常所说的层次遍历。
|
||
|
||
因为树的定义本身就是递归定义,因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁,而对于广度遍历来说,需要其他数据结构的支撑,比如队列。
|
||
|
||
## 遍历
|
||
|
||
二叉树的遍历你可能会在各种面试和算法题目中遇到。
|
||
|
||
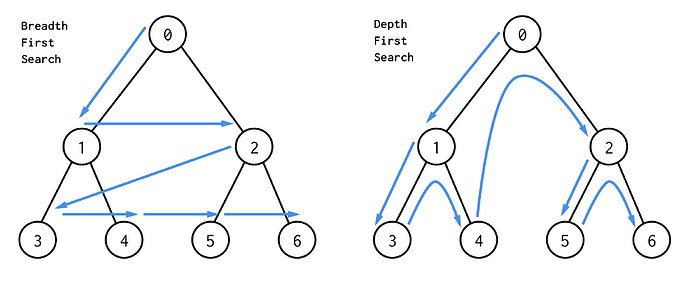
这里主要讨论下面几种种遍历算法。在遍历 深度遍历算法(depth-first search,缩写为 DFS)和 广度遍历算法(breadth-first search,
|
||
简称 BFS)
|
||
|
||
|
||
|
||
相对来说,深度遍历算法一般都可以在程序中使用递归来实现。
|
||
|
||
广度遍历算法一般都需要解借助一个其他的存储结构,一般来说会考虑使用队列来实现。
|
||
|
||
遍历的逻辑按照上面的说明的方法,使用下面 4 种遍历的方法。
|
||
|
||
(DFS)前序遍历:根结点 ---> 左子树 ---> 右子树
|
||
|
||
(DFS)中序遍历:左子树---> 根结点 ---> 右子树
|
||
|
||
(DFS)后序遍历:左子树 ---> 右子树 ---> 根结点
|
||
|
||
(BFS)层次遍历:只需按层次遍历即可
|
||
|
||
|
||
|
||
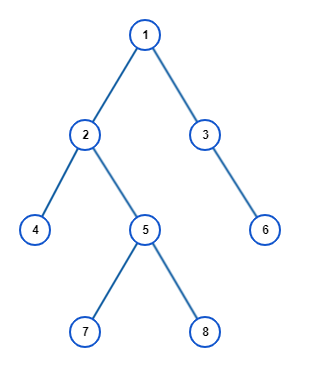
上面这个树的按照各种不同的遍历方法的遍历结果为:
|
||
|
||
前序遍历:1 2 4 5 7 8 3 6
|
||
|
||
中序遍历:4 2 7 5 8 1 3 6
|
||
|
||
后序遍历:4 7 8 5 2 6 3 1
|
||
|
||
层次遍历:1 2 3 4 5 6 7 8
|
||
|
||
针对上面的提出的各种遍历方法,我们对程序中使用的遍历代码进行分析。
|
||
|
||
首先需要将上面的数据结构初始化为数组。可以将上面的树初始化为数组:[1,2,3,4,5,#,6,#,#,7,8,#,#],这个数字中的 # 符号表示的为
|
||
NULL,就是没有子节点的意思。
|
||
|
||
### 前序遍历
|
||
|
||
递归方法,我们可以很容易的使用前序的递归来对树进行遍历。
|
||
|
||
```
|
||
/**
|
||
*
|
||
* @param root
|
||
*/
|
||
public void preOrderTraverselRecursion(TreeNode root) {
|
||
if (root != null) {
|
||
loopList.add(root.val);
|
||
preOrderTraverselRecursion(root.left);
|
||
preOrderTraverselRecursion(root.right);
|
||
}
|
||
}
|
||
```
|
||
|
||
中序遍历
|
||
|
||
```
|
||
/**
|
||
*
|
||
* @param root
|
||
*/
|
||
public void preOrderTraverselRecursion(TreeNode root) {
|
||
if (root != null) {
|
||
preOrderTraverselRecursion(root.left);
|
||
loopList.add(root.val);
|
||
preOrderTraverselRecursion(root.right);
|
||
}
|
||
``` |